Như chúng ta đã biết, tín hiệu cộng hưởng từ mạnh nhất tại thời điểm vừa tắt xung kích thích. Sau đó tín hiệu sẽ giảm dần theo thời gian, một hiện tượng mà chúng ta gọi là hiện tượng suy giảm cảm ứng tự do FID. Thế nhưng nếu chỉ đo tín hiệu một lần ngay tại thời điểm tín hiệu mạnh nhất, chúng ta gặp phải hai vấn đề sau:

1. Tín hiệu lúc này chưa có thông tin gì cho thấy sự khác biệt giữa các cấu trúc giải phẫu hay các mô khác
2. Tín hiệu lúc này chưa có thông tin gì cho phép định vị được nơi phát ra tín hiệu.

Độc giả rất có thể sẽ phản ứng ngay. Ở điểm (1), các cấu trúc khác nhau thì mật độ proton khác nhau, cho ra các tín hiệu khác nhau, sao lại nói chưa có thông tin gì về sự khác biệt giữa các cấu trúc? Ở điểm (2), nơi phát tín hiệu chính là cơ thể bệnh nhân, sao lại không định vị được?

Mấu chốt của vấn đề là, chúng ta không thể đo được tín hiệu của từng proton, cũng không thể đo được tín hiệu của từng mô hay từng cấu trúc. Chúng ta chỉ đo được tín hiệu chung, nghĩa là tín hiệu tổng hợp của toàn cơ thể. Vậy thì, làm thế nào để tín hiệu tổng hợp đó chứa đựng đủ thông tin cho phép chúng ta xác định được:

1. Các tín hiệu thành phần đã tạo ra tín hiệu tổng hợp,
2. Mỗi tín hiệu thành phần có độ lớn (cường độ) là bao nhiêu, và
3. Mỗi tín hiệu thành phần được phát ra từ đâu.

Trong phần này chúng ta sẽ tập trung vào các vấn đề có tính chất kỹ thuật, bao gồm các kỹ thuật tái lập, đo đạc và xử lý tín hiệu để tạo ra một bức ảnh cộng hưởng từ. Nội dung chủ yếu của phần bao gồm:

• Lớp cắt
• Các tính chất của ảnh cộng hưởng từ
• Mã hóa vị trí không gian
• Xử lý tín hiệu và tạo ảnh

1. LỚP CẮT

Trước khi tìm hiểu về quá trình tạo ảnh cộng hưởng từ, chúng ta cần tìm hiểu một số khái niệm liên quan đến đối tượng hay vật được chụp ảnh cộng hưởng từ. Trong phạm vi cộng hưởng từ y học, chúng ta cần chụp một vùng cơ thể của một bệnh nhân bằng cách “cắt” vùng đó thành từng lớp hay lát mỏng để có thể “nhìn thấu” vào bên trong vùng đó trong khi bệnh nhân vẫn đang “sống”. Không giống với CT chỉ cho phép cắt ngang trục, kỹ thuật cộng hưởng từ cho phép chúng ta cắt một vùng cơ thể theo một hướng bất kỳ. Ba kiểu lớp cắt cơ bản là: cắt ngang trục (axial), cắt dọc đứng (sagittal) và cắt dọc ngang (coronal). Trong cuốn sách này chúng ta không cần phân biệt từng kiểu cắt mà chỉ gọi chung là lớp cắt hay lát cắt (slice) (Hình 1).

Hình 1: Mỗi lớp cắt là một khối cơ thể cần khảo sát với một độ dày nhất định. Quang trường là phần diện tích cần khảo sát trên bề mặt của lớp cắt, có thể bao quát toàn bộ diện tích của lớp cắt (hình chữ nhật lớn) hoặc chỉ một vùng nào đó (hình chữ nhật nhỏ).

Độ dày lớp cắt

Mỗi lớp cắt có một chiều cao hay một độ dày (thickness) nhất định (Hình 1). Nghĩa là, lớp cắt không chỉ là bề mặt của vùng cơ thể cần khảo sát mà là một khối thể tích của cơ thể. Vì vậy, chụp hình một lớp cắt không phải là chụp bề mặt đơn thuần: chúng ta chụp hình cả một khối thể tích mỏng của cơ thể (lớp cắt) rồi chiếu lên một mặt phẳng, cho ra một hình trông như bề mặt của một vùng cơ thể khi bị cắt ngang.

Các lớp cắt song song với nhau thường có độ dày bằng nhau. Nếu các lớp cắt khá thưa, giữa hai lớp kế cận có thể còn một khoảng trống (Hình 2a). Khi này, khối cơ thể nằm ở khoảng trống không được chụp hình. Ngược lại, nếu các lớp cắt quá dày, chúng có thể chồng lên nhau (Hình 2c). Lý tưởng nhất là chúng ta cắt vừa phải sao cho các lớp cắt sẽ nằm sát nhau, không có khoảng trống giữa chúng (Hình 2b). Ở trường hợp này, chúng ta sẽ chụp được toàn bộ vùng cơ thể cần khảo sát mà không bỏ sót bất kỳ một phần nào.

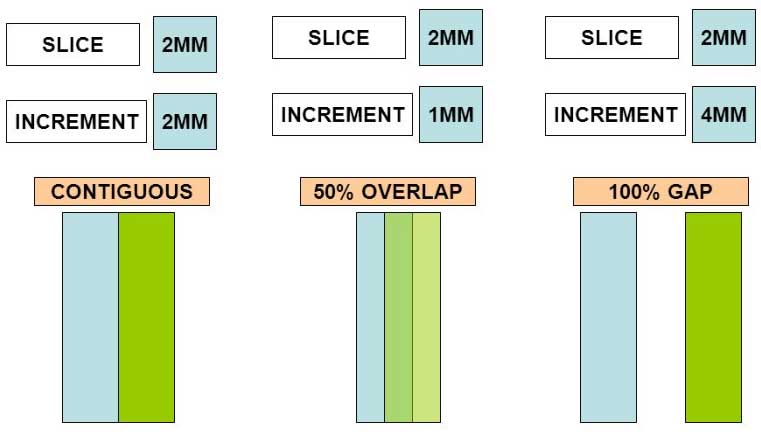
Hình 2: (a) Hai lớp kế cận nằm vừa sát với nhau, không có khoảng trống giữa chúng. (b) Hai lớp kế cận chồng lên nhau khi cắt quá dày. (c) Cắt quá thưa để lại một khoảng trống giữa hai lớp cắt kế cận.

Quang trường

Trong nhiều trường hợp chúng ta không cần khảo sát hết toàn bộ lớp cắt. Chẳng hạn khi đánh giá tình trạng thoái hóa cột sống vùng thắt lưng, chúng ta chỉ muốn khảo sát cột sống và các cấu trúc có liên quan như dây chằng, đĩa đệm, khối cơ dựng sống và hầu như bỏ qua các tạng trong ổ bụng. Trong trường hợp này nếu cắt ngang bụng, chúng ta chỉ cần tập trung chụp một vùng nhỏ bao quanh cột sống. Nếu quan sát trên bề mặt của lớp cắt, chúng ta chỉ muốn quan sát một diện tích nhỏ quanh cột sống.

Khái niệm quang trường FOV (field of view) muốn nói đến phần diện tích cần khảo sát trên bề mặt của một lớp cắt. Trong những tình huống thông thường, quang trường luôn bao quát hết toàn bộ diện tích bề mặt của lớp cắt. Tuy nhiên khi cần khảo sát tập trung một vùng, quang trường có khi chỉ chiếm một phần diện tích nhỏ. Trong thực tế, quang trường của vùng cần khảo sát được xem là diện tích hình chữ nhật bao hết vùng đó (Hình 1), tính bằng cm² hoặc mm².

Theo cách này, một lớp cắt ngang qua đầu sẽ có quang trường nhỏ hơn so với một lớp cắt ngang qua bụng; một lớp cắt dọc đứng đôi khi có quang trường lớn hơn nhiều so với lớp cắt ngang. Một quang trường lớn cho phép chúng ta đánh giá tổng thể tốt hơn nhưng có thể bỏ sót những thương tổn nhỏ. Ngược lại một quang trường nhỏ cho phép thấy được nhiều chi tiết cấu trúc rất có thể không ghi nhận được trong một quang trường lớn.

Cũng cần phân biệt quang trường với độ phóng đại (magnification). Độ phóng đại liên quan đến việc hiển thị hình ảnh trên màn hình máy tính hoặc in ra phim (thiết bị), chỉ ra rằng ảnh trên màn hình hay ảnh in ra phim có kích thước lớn hơn ảnh gốc bao nhiêu lần. 

Voxel

Với các đại lượng độ dày và quang trường, lớp cắt của chúng ta thật sự là một khối thể tích hình hộp chữ nhật (rất mỏng). Nếu chia nhỏ lớp cắt thành nhiều khối hộp nhỏ hơn nữa như được minh họa trong Hình 3, mỗi khối hình hộp chữ nhật nhỏ này sẽ có chiều cao bằng với độ dày của lớp cắt và diện tích đáy của nó chiếm một phần trong quang trường. Chúng ta gọi mỗi khối hình hộp là một phần tử thể tích hay voxel (volume element).

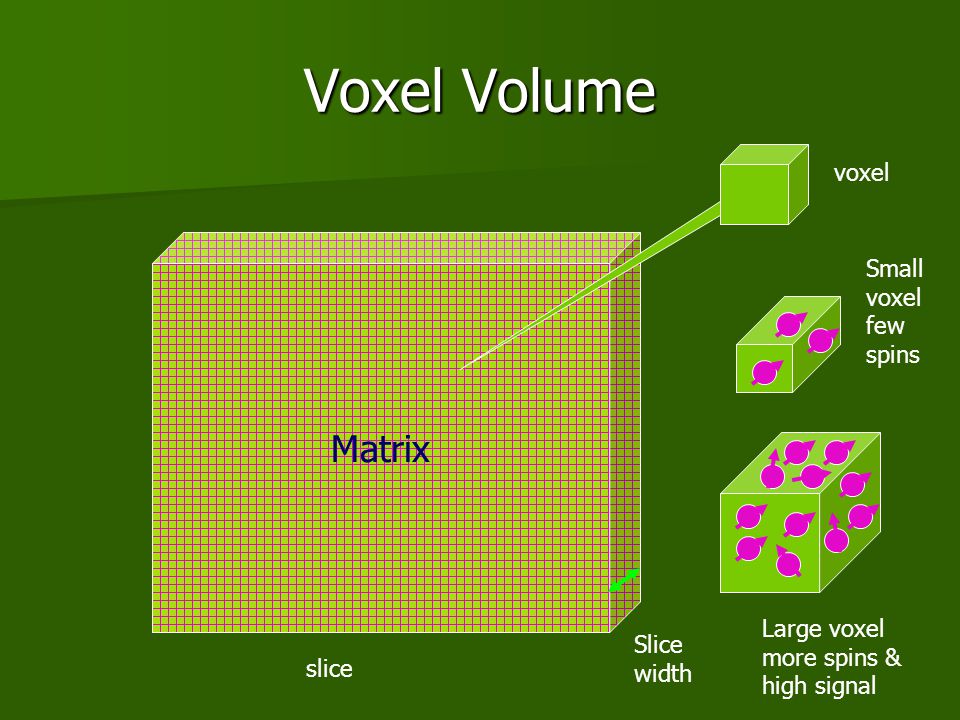
Hình 3: Voxel là một khối thể tích nhỏ của lớp cắt có chiều cao bằng độ dày của lớp cắt và diện tích đáy được xem là kích thước của một pixel.

Rõ ràng, thể tích của voxel phụ thuộc vào mức độ chia nhỏ lớp cắt. Với một lớp cắt nhất định, nếu chúng ta chia lớp cắt thành nhiều voxel thì thể tích của mỗi voxel sẽ giảm đi; ngược lại nếu chia thành ít voxel hơn, thể tích của voxel sẽ lớn hơn. Giả sử một lớp cắt có độ dày 5mm và quang trường của nó có diện tích 200 x 200 = 40.000 mm². Nếu chúng ta chia lớp cắt này thành 65.536 voxel, mỗi voxel khi đó sẽ có thể tích 3 mm³. Ngược lại nếu chia lớp cắt thành nhiều voxel hơn, chẳng hạn 100.000 voxel, thể tích mỗi voxel khi này sẽ là 2 mm².

2. CÁC TÍNH CHẤT CỦA HÌNH CỘNG HƯỞNG TỪ

Sau khi đã tìm hiểu các đại lượng biểu thị cho bản thân vật được chụp hình như lớp cắt, độ dày lớp cắt, quang trường và voxel, trong phần này chúng ta sẽ xem xét các tham số được biểu thị trên hình khi chúng được quy gán từ các đại lượng đã nêu.

Pixel và ma trận ảnh

Khi đo tín hiệu cộng hưởng từ, chúng ta không thể phân định được tín hiệu của từng proton mà chỉ phân định được tín hiệu chung của các proton trong một đơn vị thể tích. Đơn vị thể tích mà chúng ta dùng để quy gán tín hiệu chính là voxel. Khi tạo ảnh, tín hiệu chung của các proton trong một voxel được biểu thị bằng một điểm ảnh: cứ một voxel sẽ có một điểm ảnh tương ứng. Chúng ta gọi mỗi điểm ảnh như thế là một phần tử ảnh hay pixel (picture element).

Kích thước của mỗi pixel được xem là phần diện tích của voxel tương ứng khi nó bộc lộ trên bề mặt của lớp cắt (Hình 3). Tổng diện tích của các pixel chính là quang trường. Chẳng hạn với lớp cắt có độ dày 5 mm và quang trường 40.000 mm2 trong thí dụ ở phần trước, khi lớp cắt được chia thành 65.536 voxel, tương ứng với 65.536 pixel, diện tích của mỗi pixel khi đó sẽ là 0,6 mm2.

Theo quy ước, quang trường là một hình chữ nhật. Vì thế để dễ đối chiếu trên hình, người ta mô tả số lượng pixel dưới dạng ma trận ảnh (image matrix). Cụ thể, một ma trận ảnh n x m muốn nói rằng ảnh có n hàng và m cột pixel. Nghĩa là nếu đếm trên một hàng, ảnh có m pixel còn nếu đếm trên một cột, ảnh có n pixel. Tổng số pixel của ảnh được tính bằng cách lấy n nhân với m. Chẳng hạn nếu một ảnh được mô tả bằng ma trận ảnh 256 x 128, chúng ta biết rằng có cả thảy 256 x 128 = 32.768 pixel được xếp sát vào 256 hàng và 128 cột.

Hình 4 minh họa hai ma trận ảnh có quang trường bằng nhau nhưng có số lượng pixel khác nhau. Vì mỗi voxel được biểu thị bằng một pixel trên hình nên với một quang trường nhất định, khi số pixel càng lớn, kích thước mỗi pixel càng nhỏ. Nếu biết được cả độ dày lớp cắt, chúng ta có thể tính ra thể tích tương ứng của mỗi voxel. Do vậy đối với một lớp cắt nhất định có quang trường và độ dày đã biết, ma trận ảnh của nó cho chúng ta hình dung kích thước của mỗi voxel mà như chúng ta sẽ phân tích tiếp trong đoạn sau, kích thước của voxel có liên quan mật thiết đến khả năng phân định chi tiết các cấu trúc giải phẫu. Cụ thể hơn, khi thể tích voxel càng nhỏ, chi tiết các cấu trúc càng rõ nét.

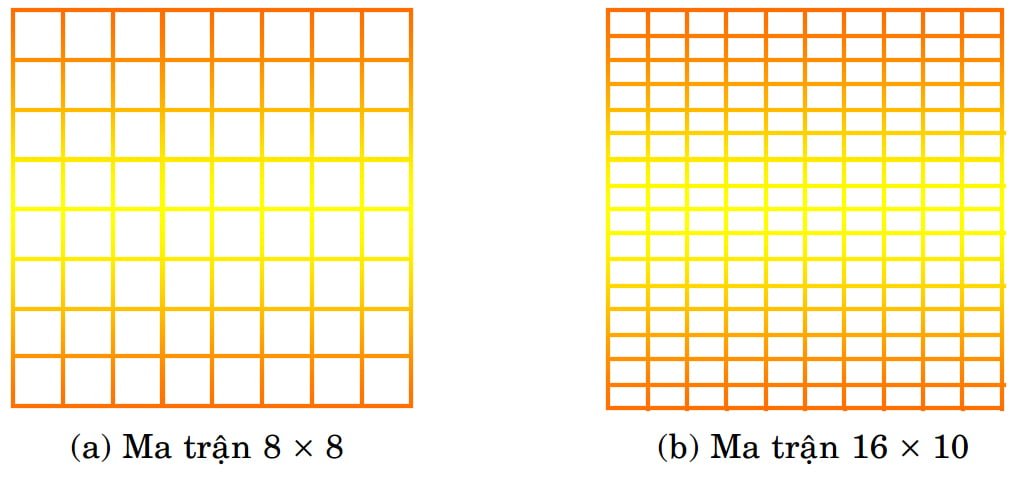
Hình 4: Pixel và ma trận ảnh. Quang trường của hai hình đều bằng nhau. (a) Một ma trận ảnh 8 x 8 có 64 pixel, được sắp thành 8 hàng và 8 cột. (b) Ma trận 16 x 10 có diện tích bề mặt (quang trường) bằng với (a) nhưng do số pixel tăng lên (160 pixel) nên kích thước của mỗi pixel giảm đi.

Độ phân giải không gian

Khi thực hiện khảo sát một vùng cơ thể bằng cộng hưởng từ, chúng ta muốn có khả năng phân định vùng khảo sát càng chi tiết càng tốt. Mức chi tiết của vùng cần khảo sát mà hệ thống cộng hưởng từ có thể phân định được gọi là độ phân giải không gian (spatial resolution). Độ phân giải không gian là một chỉ số quan trọng khi đánh giá chất lượng của một hình ảnh cộng hưởng từ. Một hình cộng hưởng từ có độ phân giải không gian cao cho chúng ta biết rằng chi tiết của vùng đang khảo sát được ghi nhận tốt hơn. Kết quả là:

1. Số lượng các cấu trúc nhỏ có thể ghi nhận được sẽ tăng lên
2. Mỗi cấu trúc sẽ được hiển thị rõ nét hơn, và
3. Ranh giới giữa các cấu trúc sẽ rõ ràng hơn.

Mặt khác, khi đo tín hiệu cộng hưởng từ, mỗi voxel được xem như một đơn vị quy gán tín hiệu: tín hiệu của các proton trong một voxel sẽ được tính bình quân để cho ra một tín hiệu chung. Nghĩa là chúng ta có thể xem voxel là mức chi tiết nhỏ nhất mà chúng ta phân định được tín hiệu từ đó phát ra.

Tuy nhiên do tín hiệu chung được lấy bình quân, nó là giá trị “cào bằng”. Nghĩa là mọi proton trong voxel được xem như chỉ phát ra tín hiệu chung đó. Giá trị cào bằng này sẽ ít đại diện cho tín hiệu của từng proton có trong voxel nếu thể tích voxel quá lớn bởi lẽ khi đó, một voxel có nhiều khả năng chứa nhiều loại mô khác nhau. Nếu bản thân các phần mô nằm trong một voxel có cường độ tín hiệu khác biệt quá lớn, tín hiệu chung của chúng sẽ cào bằng sự khác biệt này, biểu hiện như thể toàn bộ voxel chỉ có một cấu trúc đồng nhất. Khi đó, ranh giới giữa các mô trong vùng đang khảo sát bị xóa mờ không còn rõ nét nữa.

Do vậy, mức chi tiết của vùng khảo sát phụ thuộc vào thể tích voxel. Nghĩa là độ phân giải không gian được biểu thị hoàn toàn bằng thể tích voxel: thể tích voxel càng nhỏ, độ phân giải không gian càng cao.

Khẳng định vừa nêu ở trên cho phép chúng ta lượng hóa khái niệm độ phân giải bằng thể tích voxel và có thể tính được độ phân giải dựa trên các tham số độ dày lớp cắt, quang trường và ma trận ảnh. Về mặt định tính, chúng ta có thể đưa ra một số kết luận quan trọng:

1. Với một quang trường nhất định và độ dày lớp cắt nhất định, số pixel trong một ma trận ảnh càng nhiều, độ phân giải không gian càng cao, cho ra ảnh càng sắc nét.
2. Với một quang trường nhất định và ma trận ảnh nhất định, lớp cắt càng dày, độ phân giải không gian càng thấp, cho ra ảnh càng nhòe.

Tỷ lệ tín hiệu / nhiễu

Tín hiệu cộng hưởng từ phát ra từ các voxel mà chúng ta thu nhận được không phải là tín hiệu “tinh khiết”. Môi trường xung quanh có thể sinh ra một lượng tín hiệu nhỏ đi kèm với tín hiệu được phát ra từ voxel. Lượng tín hiệu không mong muốn này được gọi là độ nhiễu (noise). Nếu độ nhiễu cao, tín hiệu thu được sẽ không chính xác, tạo ra hình ảnh không trung thực. Thế nhưng, đo đạc và tính toán được độ nhiễu thường mất rất nhiều công sức và rất khó thực hiện. Thực sự là, tỷ lệ tín hiệu/nhiễu hay tỷ lệ SNR (signal to noise ratio), nghĩa là độ lớn của tín hiệu thực so với độ nhiễu, có ý nghĩa thực tiễn hơn bản thân độ nhiễu. Tỷ lệ SNR càng lớn, độ trung thực của ảnh càng cao.

Trong kỹ thuật chụp cộng hưởng từ, tỷ lệ SNR là một tham số rất quan trọng. Để có được hình ảnh với độ trung thực cao, chúng ta phải đo được tín hiệu có tỷ lệ SNR cao. Nghĩa là chúng ta phải cố gắng để làm tăng tỷ lệ SNR càng nhiều càng tốt. Mặt khác, để có hình ảnh chi tiết và sắc nét, nghĩa là hình ảnh có độ phân giải không gian cao, chúng ta cần phải giảm thiểu kích thước của voxel xuống càng nhiều càng tốt.

Mới nghe qua, chúng ta thấy rằng cả hai yêu cầu này hoàn toàn hợp lý và chẳng có gì mâu thuẫn với nhau. Muốn có độ trung thực cao, cần tăng tỷ lệ SNR; để có độ phân giải tốt, hãy giảm thể tích voxel.

Thế nhưng khi giảm thể tích voxel, tỷ lệ SNR cũng giảm. Nghĩa là tỷ lệ SNR tỷ lệ thuận với thể tích voxel. Khi thể tích voxel tăng lên, lượng tín hiệu thực sự của voxel đủ mạnh để “phủ quyết” những ảnh hưởng của nhiễu, làm cho độ trung thực của ảnh tăng lên. Do vậy trong thực tế, các hệ thống chụp ảnh cộng hưởng từ sẽ phải cân đối giữa nhu cầu có độ phân giải cao với nhu cầu có được độ trung thực của ảnh để có được một chọn lựa tối ưu.

Ở một mức nào đó, giải pháp tối ưu được chọn còn có liên quan đến cường độ từ trường B₀ và thời gian đo tín hiệu (acquisition time) bởi vì tỷ lệ SNR cũng phụ thuộc vào từ trường ngoài B₀ và thời gian đo này. Vì đây là những vấn đề có tính chất kỹ thuật nên chúng ta không đi quá sâu vào chi tiết. Chúng ta chỉ đơn giản đưa ra một kết luận quan trọng cần ghi nhớ: Một máy cộng hưởng từ có từ trường mạnh hơn sẽ tạo ra hình ảnh cộng hưởng từ có chất lượng tốt hơn.

Hiển thị ảnh

Sau khi đã tìm hiểu xong các tham số quan trọng trên hình chụp của một lớp cắt, bây giờ chúng ta tìm hiểu việc hiển thị hình chụp đó ra màn hình hoặc in ra phim. Cần nhớ rằng khái niệm ảnh mà chúng ta vừa bàn luận ở trên được xem là ảnh gốc với “kích cỡ” thật. Khi hiển thị trên thiết bị (màn hình hoặc xuất ra phim), vì nhiều lý do chúng ta không thể hiển thị ảnh gốc với kích cỡ thật của nó. Thay vì thế, các tham số của ảnh gốc sẽ được quy đổi để có thể hiển thị nó tốt nhất trên thiết bị. Ảnh khi này được gọi là ảnh thiết bị (device image) để phân biệt với ảnh gốc.

Trước tiên chúng ta cần biết rằng các thiết bị như màn hình máy tính và máy in cũng hiển thị ảnh theo từng chấm nhỏ xíu. Những chấm này cũng được gọi là điểm ảnh hay pixel, và để phân biệt với pixel của ảnh gốc, người ta gọi đó là pixel thiết bị (device pixel). Đối với máy in, pixel thường được gọi là dot, nghĩa là các điểm chấm nhỏ nhất mà máy in có thể in ra được. Kích thước của pixel thiết bị dĩ nhiên phụ thuộc vào từng thiết bị.

Tương tự như độ phân giải không gian của ảnh gốc biểu thị khả năng phân định chi tiết các cấu trúc của lớp cắt được chụp, độ phân giải thiết bị (device resolution) biểu thị khả năng hiển thị của thiết bị. Như thế, độ phân giải thiết bị chính là số pixel thiết bị có thể hiển thị được trên một đơn vị diện tích. Số pixel có thể hiển thị được càng nhiều, độ phân giải càng cao. Theo thông lệ, độ phân giải được ghi dưới dạng ma trận (đối với màn hình) hoặc số dpi (dots per inch, số điểm chấm trên mỗi inch). Chẳng hạn đối với màn hình, độ phân giải 800 x 600 rõ ràng thấp hơn độ phân giải 1024 x 768; đối với máy in laser, độ phân giải 600 dpi chắc chắn cao hơn độ phân giải 300 dpi.

Nếu mỗi pixel của ảnh gốc được hiển thị bằng một pixel thiết bị, ảnh đó là ảnh chính xác và trung thực nhất. Tuy nhiên một ảnh thiết bị như thế thường gây khó khăn cho chúng ta khi cần phân định chi tiết của cấu trúc vì bản thân nó khá nhỏ, đặc biệt khi thiết bị có độ phân giải cao. Trong nhiều trường hợp, chúng ta cần phóng to ảnh lên nhiều lần để có thể nhìn rõ những cấu trúc nhỏ. Khi đó, một pixel của ảnh gốc sẽ được hiển thị bằng nhiều pixel thiết bị.

Với một độ phóng đại vừa phải, ảnh được hiển thị cho phép nhìn rõ hơn nhiều cấu trúc vì lúc này mắt vẫn thấy ảnh còn sắc nét. Tuy nhiên đến một độ phóng đại nào đó, ảnh bắt đầu bị “vỡ” vì khi đó mắt đã có thể phân biệt được từng pixel ảnh gốc do nó được hiển thị bằng “quá nhiều” pixel thiết bị.

Kết luận

Đến đây chúng ta đã tìm hiểu xong những tính chất quan trọng của ảnh: khởi đi từ những đại lượng của lớp cắt (độ dày, quang trường, voxel), quy gán chúng thành các tham số của ảnh gốc (pixel, ma trận ảnh, độ phân giải không gian) rồi hiển thị bằng ảnh thiết bị trên màn hình hoặc trên phim (máy in). Chúng ta tóm tắt một số kết luận quan trọng như dưới đây:

1. Độ phân giải không gian biểu thị mức độ chi tiết của các cấu trúc giải phẫu biểu hiện được trên hình. Độ phân giải càng cao, khả năng biểu hiện chi tiết càng tốt và ảnh càng sắc nét.
2. Vì voxel được xem là đơn vị thu nhận tín hiệu, thể tích của voxel là một chỉ số quyết định độ phân giải không gian: thể tích voxel càng nhỏ, độ phân giải không gian càng cao.
3. Thể tích voxel có thể tính được nếu biết độ dày của lớp cắt và kích thước của pixe Với một quang trường và một độ dày đã cho, nếu chia quang trường thành nhiều pixel thì kích thước pixel giảm, dẫn đến thể tích voxel giảm. Ngược lại nếu quang trường và số pixel giữ cố định thì lớp cắt càng mỏng, thể tích voxel càng nhỏ.
4. Khi giảm thể tích voxel, tỷ lệ SNR, vốn là một chỉ số biểu thị mức độ trung thực của ảnh, càng giả Do vậy chúng ta cần phải cân đối giữa yêu cầu ảnh có độ trung thực cao với yêu cầu ảnh biểu hiện được nhiều chi tiết.
5. Ảnh gốc được hiển thị trung thực nhất khi mỗi pixel của ảnh được hiển thị bằng một pixel thiết bị.

3. MÃ HÓA VỊ TRÍ KHÔNG GIAN

Như chúng ta đã phân tích trong phần mở đầu của phần này, tín hiệu cộng hưởng từ thu được từ thiết bị đo sóng radio chỉ là tín hiệu tổng hợp từ các tín hiệu được các voxel phát ra. Nếu dùng một thiết bị tách tín hiệu, chúng ta có thể phân định được các tín hiệu thành phần đã tạo ra tín hiệu tổng hợp nhưng không thể biết được voxel nào đã phát ra tín hiệu nào, nghĩa là không thể định vị được nơi đã phát ra tín hiệu bởi vì chẳng có thông tin gì cho biết vị trí tín hiệu.

Muốn biết được vị trí của voxel đã phát ra tín hiệu, chúng ta cần đưa thêm thông tin vị trí vào từng tín hiệu. Nói theo từ ngữ kỹ thuật, chúng ta cần mã hóa vị trí của voxel ngay trong từng tín hiệu thành phần, nghĩa là cần tìm cách biểu diễn tọa độ không gian ba chiều của voxel trong từng tín hiệu.

Thế nhưng như chúng ta đã biết, tín hiệu cộng hưởng từ là một loại sóng điện từ, vì vậy nó có ba tham số đặc trưng: tần số, pha và biên độ, trong đó biên độ chính là độ lớn hay cường độ tín hiệu. Vì vậy chúng ta có thể mã hóa thông tin vị trí vào hai tham số còn lại là tần số và pha.

Trong phần này, chúng ta sẽ tìm cách mã hóa thông tin vị trí vào tần số và pha. Sau đó từ sự khác biệt về tần số và pha của các tín hiệu, chúng ta có thể suy ra được vị trí của voxel đã phát ra tín hiệu đó. Cuối cùng dựa vào biên độ chúng ta có thể tái hiện lại “hình ảnh” của voxel một cách trung thực nhất.

Thang từ trường

Để có thể mã hóa thông tin vị trí vào tần số và pha, trước tiên chúng ta cần tìm hiểu về khái niệm thang từ hay gradient từ (field gradient). (Gradient theo nghĩa gốc là “chiều hướng thay đổi” của một đại lượng vật lý và thường được để nguyên không dịch. Ở đây chúng tôi vẫn tìm cách dịch thuật ngữ này và nhiều thuật ngữ khác ra tiếng Việt, với ý định cụ thể là giúp độc giả có thể hiểu được các vấn đề được nêu ra một cách dễ dàng và rõ ràng hơn). Thang từ hay gradient từ là một dãy các từ trường có cường độ thay đổi dần theo một trục trong không gian. Trong các hệ thống chụp ảnh cộng hưởng từ, thang từ có thể thay đổi từ mức ngược chiều với từ trường ngoài B₀ đến mức cùng chiều với từ trường ngoài B₀ (Hình 5).

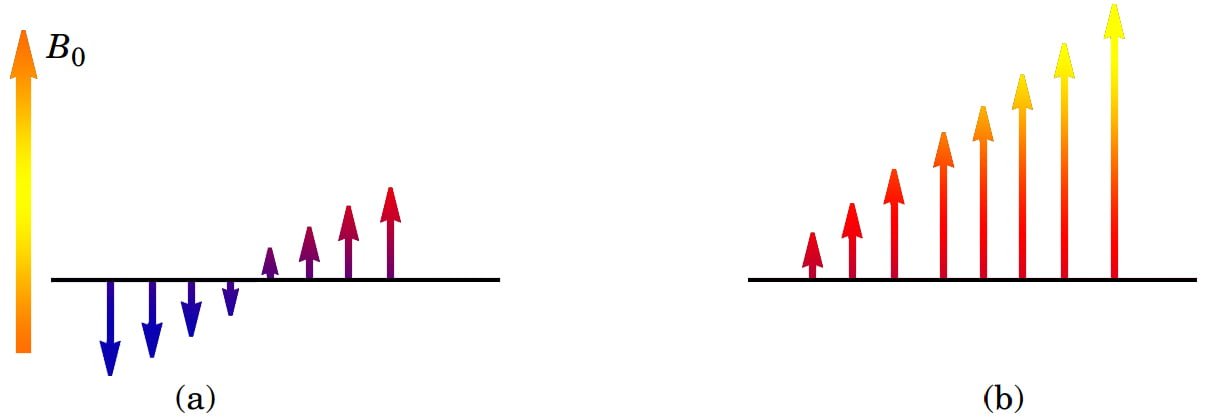
Hình 5: (a) Từ trường ngoài B₀ và thang từ trường tác động theo một trục nằm ngang. (b) Lực tác động tổng hợp giữa B₀ và thang từ làm cho mỗi mặt phẳng dọc theo trục nằm ngang này chịu tác động của một từ trường khác nhau. Các từ trường này thay đổi một cách có hệ thống, có thể từ mức ngược chiều với từ trường ngoài B₀ đến mức thuận chiều với nó.

Kết quả là theo trục biến đổi của thang từ, từ trường thực sự tại mỗi mặt phẳng vuông góc với trục cũng biến đổi một cách có hệ thống, có thể thay đổi từ thái cực ngược chiều với từ trường ngoài B₀ đến thái cực cùng chiều với nó, cho phép chúng ta kiểm soát được từ trường thực sự tác động lên mỗi voxel cần khảo sát.

Thang từ chọn lớp Gs

Để thực hiện mã hóa thông tin vị trí vào tín hiệu, trước tiên chúng ta cần chọn được lớp cắt cần chụp sao cho chỉ các proton trong các voxel của lớp cắt này mới phát ra tín hiệu; proton trong các voxel của các lớp cắt khác không bị kích thích và vì vậy không tạo ra tín hiệu cộng hưởng từ.

Muốn vậy, chúng ta sử dụng một thang từ thích hợp. Dưới tác động của thang từ tổng hợp của từ trường ngoài B₀ và thang từ này, proton trong các voxel của mỗi lớp cắt vuông góc với thang từ trường sẽ quay với một tần số khác nhau theo phương trình Larmor,

f = γB

trong đó B là cường độ từ trường tổng hợp của B₀ và thang từ tác động tại mặt phẳng chứa proton và vuông góc với trục ngang.

Vì thang từ thay đổi có quy luật, chúng ta có thể phát ra một xung kích thích có tần số chỉ thích hợp với lớp cắt cần khảo sát, nghĩa là chỉ các proton trong lớp cắt cần khảo sát mới có tần số quay cộng hưởng được với xung kích thích. Bằng cách này, sau khi tắt xung kích thích, chỉ có các voxel trong lớp cắt này mới phát ra tín hiệu cộng hưởng từ.

Như vậy để chọn một lớp cắt, chúng ta sẽ áp đặt một thang từ, được gọi là thang từ chọn lớp hay thang chọn lớp (slice selection gradient, ký hiệu là Gs) trước khi phát xung kích thích. Dưới tác động của thang chọn lớp, proton trong các mặt phẳng dọc vuông góc với trục của thang từ sẽ có tần số cộng hưởng khác nhau tùy theo vị trí của proton trên trục này. Khi đó nếu phát một xung kích thích có tần số phù hợp với tần số cộng hưởng của các proton trong lớp cắt cần khảo sát thì tín hiệu được phát ra chính là tín hiệu của các proton này.

Bằng cách phối hợp các thang chọn lớp, chúng ta có thể khảo sát trực tiếp cơ thể theo nhiều lớp cắt ở nhiều góc độ khác nhau, không chỉ là cắt ngang trục, cắt dọc đứng hay cắt dọc ngang. Đây được xem là một trong những ưu điểm quan trọng nhất của kỹ thuật chụp ảnh cộng hưởng từ.

Thang từ mã hóa bằng tần số Gf

Bây giờ trong lớp cắt cần khảo sát, chúng ta cần mã hóa vị trí (tọa độ) của các voxel theo một hệ trục vuông góc: một trục được mã hóa bằng tần số và trục còn lại được mã hóa bằng pha của tín hiệu được phát ra từ mỗi voxel. Trước tiên chúng ta xem xét khả năng mã hóa vị trí bằng tần số.

Sau khi đã kích thích lớp cắt cần khảo sát bằng một xung thích hợp dưới tác động của một thang chọn lớp Gs, tín hiệu đo được chính là tín hiệu được phát ra từ các voxel trong lớp cắt đó. Bây giờ để mã hóa vị trí các voxel theo một trục trong mặt phẳng của lớp cắt đang khảo sát, chúng ta áp dụng một thang từ dọc theo trục đó, gọi là trục tần số (Hình 6). Thang từ được dùng với mục đích này gọi là thang từ mã hóa bằng tần số hay thang mã tần (frequency coding gradient, ký hiệu là Gf). Tác dụng của nó là làm cho tần số của các proton trong các voxel dọc theo trục đó thay đổi một cách có hệ thống. Nghĩa là dọc theo trục, các proton trong các voxel ở một đầu sẽ quay chậm; các proton trong các voxel kế cận theo trục đó sẽ quay nhanh hơn, và cứ như thế cho đến đầu kia của trục, các proton trong các voxel ở đầu tận còn lại sẽ quay nhanh nhất. Kết quả là tần số tín hiệu được phát ra từ các voxel dọc theo trục cũng thay đổi một cách có hệ thống: ở một đầu, tần số thấp rồi tăng dần cho đến đầu kia có tần số cao.

Vì tần số của các voxel thay đổi một cách tuyến tính theo khoảng cách nên từ tần số của mỗi voxel, chúng ta có thể suy ra vị trí của nó trên trục tần số. Nói cách khác, thông tin vị trí của theo trục tần số đã được mã hóa vào tần số của voxel.

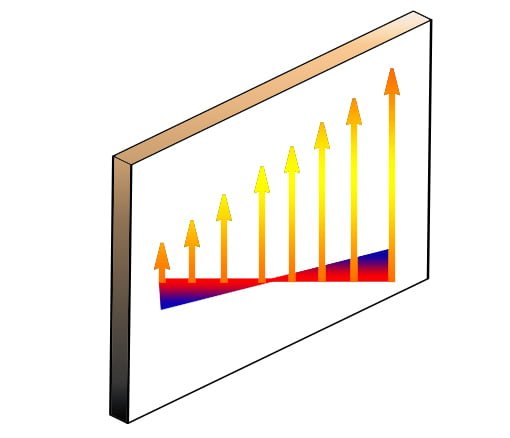
Hình 6: Thang từ mã hóa bằng tần số Gf làm thay đổi tần số của các proton trong các voxel dọc theo trục của thang từ theo cách làm cho tần số biến thiên dần từ thấp đến cao dọc theo trục đó. Dựa trên tần số của tín hiệu, chúng ta có thể xác định được vị trí voxel: tín hiệu có tần số thấp là của các voxel nằm ở một đầu, tín hiệu có tần số cao hơn là của các voxel nằm cách xa hơn, ở phía đầu còn lại của trục tần số.

Thang từ mã hóa bằng pha Gp

Để mã hóa tọa độ của các voxel theo trục còn lại trong lớp cắt cần khảo sát, chúng ta sẽ thay đổi pha của các proton trong các voxel, cũng bằng cách dùng một thang từ. Thang từ này, được gọi là thang từ mã hóa bằng pha hay thang mã pha (phase encoding gradient, ký hiệu là Gp), được thiết lập vuông góc với thang mã tần trong mặt phẳng của lớp cắt. Về cơ bản, thang mã pha cũng có tác dụng giống như thang mã tần, nghĩa là nó cũng làm thay đổi tần số của các voxel dọc theo trục tác dụng của nó (trục pha) một cách tuyến tính: ở một đầu, tần số thay đổi ít, dần dần đến đầu kia, tần số thay đổi nhiều.

Tuy nhiên cách áp dụng thang mã pha khác với cách áp dụng thang mã tần ở hai điểm:

1. Thang mã pha chỉ được áp dụng trong một thời gian rất ngắn. Với cách làm này, tần số của proton trong các voxel dọc theo trục pha bị thay đổi một cách tuyến tính sẽ làm cho pha cũng thay đổi theo một cách tuyến tính. Thế nhưng do chỉ được áp dụng trong một thời gian rất ngắn, tần số vừa bị thay đổi sẽ nhanh chóng trở về tần số cũ sau khi tắt thang từ, trong khi đó sự thay đổi về pha lại vẫn giữ nguyên, cho phép mã hóa thông tin vị trí của voxel theo trục pha vào pha của các prôtn.
2. Ở mỗi lần áp dụng, cường độ và chiều áp dụng của thang mã pha cũng thay đổi một cách tuyến tính. Chẳng hạn ở lần áp dụng thứ nhất, cường độ mạnh nhất và theo chiều â Ở lần áp dụng thứ hai, cường độ yếu hơn theo chiều âm, giảm dần cường độ theo chiều âm cho đến zero ở những lần áp dụng tiếp theo rồi tăng dần cường độ theo chiều dương cho đến lần áp dụng cuối cùng. Như vậy sự thay đổi về pha mạnh nhất ở lần áp dụng đầu tiên và cuối cùng, trong khi đó sự thay đổi về pha yếu nhất (nghĩa là không thay đổi) xảy ra ở lần áp dụng chính giữa. Lý do phải thay đổi cường độ thang mã pha qua các lần áp dụng có liên quan đến các thuật toán xử lý tín hiệu số nên không được bàn luận thêm ở đây.

Tổng kết

Nói tóm lại, để xác định được vị trí của các voxel đã phát ra tín hiệu, trước tiên cần thực hiện một thang chọn lớp Gs sao cho chỉ có các proton trong lớp cắt cần khảo sát mới có tần số cộng hưởng được với xung kích thích. Tiếp theo là áp dụng thang mã pha Gp theo một trục trong mặt phẳng của lớp cắt. Thang từ này được thực hiện thật nhanh, làm cho pha của các proton trong lớp cắt thay đổi tùy theo vị trí của chúng dọc theo trục áp dụng thang từ. Cuối cùng là áp dụng một thang mã tần Gf trong mặt phẳng lớp cắt và vuông góc với thang mã pha Gp, làm thay đổi tần số của các proton theo trục này. Nếu tín hiệu được ghi nhận tại thời điểm này thì đây là tín hiệu của các proton trong lớp cắt cần khảo sát với các thông tin tần số và pha cho biết vị trí của chúng theo hai trục vuông góc với nhau trong mặt phẳng lớp cắt.

Bây giờ, sau khi đã xem qua rất nhiều khái niệm căn bản của kỹ thuật chụp ảnh cộng hưởng từ, chúng ta tổng kết chúng trong một diễn biến chung như sau để độc giả hình dung được bức tranh tổng thể về toàn bộ quá trình chụp ảnh cộng hưởng từ:

1. Áp dụng một từ trường ngoài thật mạnh B₀ theo trục dọc của cơ thể (gọi là trục z). Sau đó tùy theo hướng của lớp cắt cần khảo sát (cắt ngang, cắt dọc đứng hoặc cắt dọc ngang), một thang chọn lớp Gs thích hợp được áp dụng. Lúc này, các proton của các lớp cắt khác nhau sẽ có tần số quay khác nhau.
2. Phát một xung kích thích có tần số phù hợp với tần số cộng hưởng của các proton trong lớp cắt định khảo sá Xung kích thích này sẽ được lập lại sau một khoảng thời gian gọi là thời kích TR. Thời kích TR được chọn tùy thuộc vào việc chúng ta muốn có hình trọng T1, trọng T2 hoặc trọng đậm độ proton. Chú ý rằng mỗi xung kích thích này cũng hàm chứa cả góc lật a, biểu thị cho lượng vectơ từ hóa dọc bị lật thành vectơ từ hóa ngang.
3. Sau đó tắt xung kích thích và áp dụng thật nhanh thang mã pha Gp để làm thay đổi pha của các proton, biểu diễn thông tin vị trí của voxel theo trục của thang từ này dựa vào pha của các tín hiệu.
4. Tại thời điểm TE/2, nghĩa là khoảng một nửa thời vang TE, chúng ta có thể phát ra một xung tái lập 180o, nhờ đó đến thời điểm đo tín hiệu (thời vang TE), chúng ta có được một điểm vang (echo) tốt nhất.
5. Gần đến thời vang TE, chúng ta áp dụng một thang mã tần Gf, làm thay đổi tần số của các proton theo trục này để biểu diễn thông tin vị trí của các voxel theo trục đó.
6. Cuối cùng đến thời vang TE, chúng ta thực hiện đo tín hiệu. Sau khi tách các tín hiệu thành phần được phát ra từ các voxel, chúng ta có thể dựa vào tần số và pha của chúng để suy ra vị trí của voxel tương ứn Cần nhớ rằng thời vang TE được chọn tùy theo các đặc tính tương phản chúng ta muốn có trên hình.

Với sự phát triển mạnh mẽ của tin học cùng với các kỹ thuật xử lý bằng máy tính (computer), các bước được thực hiện ở trên đều được lập trình sẵn. Đặc biệt, quá trình xử lý tín hiệu và tạo ảnh cộng hưởng từ đều do máy tính thực hiện. Chúng ta sẽ tìm hiểu sơ qua về quá trình này trong Phần 4 tiếp theo sau.

Cũng cần nhấn mạnh rằng trong thực tế, các thang từ thường có cường độ rất nhỏ so với từ trường chính B₀ nhưng hoàn toàn đủ mạnh để làm thay đổi tần số hoặc pha của tín hiệu.

4. XỬ LÝ TÍN HIỆU VÀ TẠO ẢNH

Trong phần này, chúng ta tập trung vào Bước (6) được nêu ở trên, nghĩa là bước đo tín hiệu, xử lý và tạo ảnh cộng hưởng từ. Tuy nhiên do quá trình này được xử lý bằng máy tính, nghĩa là toàn bộ quá trình này đều sử dụng kỹ thuật số hóa nên bước cuối cùng không hoàn toàn giống như đã được mô tả ở trên. Trước tiên hệ thống chụp ảnh phải lấy mẫu để thực hiện số hóa tín hiệu. Sau đó mỗi mẫu sẽ được chuyển thành một con số tương ứng với giá trị của tín hiệu được lấy mẫu rồi được điền vào một bảng hai chiều có tên gọi là k-không gian. Bằng cách sử dụng một phương pháp biến đổi gọi là biến đổi Fourier, k-không gian này sẽ được chuyển thành ma trận ảnh đã được giới thiệu trong Phần 2. Ma trận ảnh chứa đủ thông tin cần thiết để máy tính hiển thị ảnh ra màn hình hoặc máy in ghi lại ảnh trên phim.

Lấy mẫu và số hóa tín hiệu

Khi tín hiệu cộng hưởng từ được phát ra từ lớp cắt đang được khảo sát, nó sẽ được đo và lấy mẫu. Cần nhớ rằng đây là tín hiệu tổng hợp chung của tất cả các tín hiệu thành phần có nguồn gốc từ các voxel có trong lớp cắt. Thay vì tách tín hiệu tổng hợp ra thành các tín hiệu thành phần, phương pháp xử lý bằng máy tính sẽ lấy mẫu tín hiệu (signal sampling): đo tín hiệu ở nhiều thời điểm khác nhau và gọi giá trị đo được là một mẫu (sample).

Trong Hình 7 chúng ta có một tín hiệu đang được lấy mẫu. Mỗi chấm đen là một mẫu được lấy tại một thời điểm nhất định. Nói cách khác, mỗi chấm đen là một giá trị của tín hiệu được đo tại một thời điểm. Tập hợp các mẫu này phác họa “hình thái” của tín hiệu đang được lấy mẫu, cho phép chúng ta tái lập tín hiệu ban đầu nếu cần.

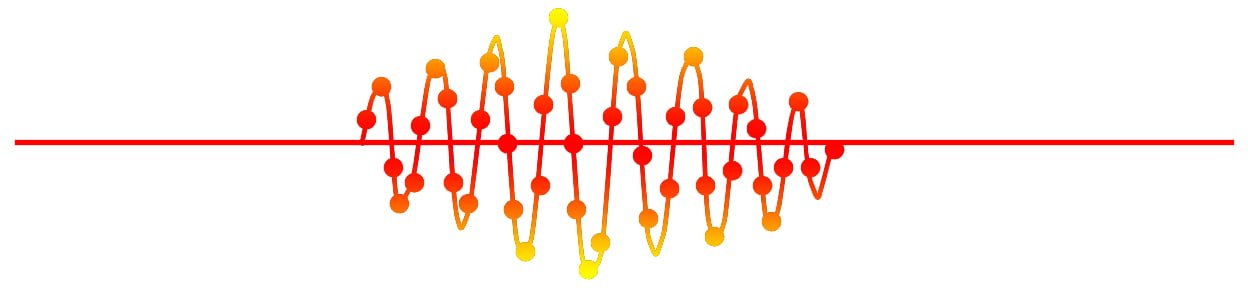
Hình 7: Tín hiệu cộng hưởng từ và các mẫu. Mỗi chấm đen là một mẫu (một giá trị) chứa thông tin về tín hiệu tại thời điểm được lấy. Mỗi mẫu này sẽ được chuyển thành một con số tương ứng với giá trị đo được của mẫu. Quá trình này được gọi là quá trình số hóa tín hiệu.

Mỗi mẫu sau đó sẽ được biến đổi thành một con số mà trong máy tính chúng được lưu dưới dạng nhị phân (binary). Quá trình lấy mẫu và biến đổi này được gọi là số hóa tín hiệu (signal digitalization). Như vậy trong phương pháp xử lý ảnh số, tín hiệu tổng hợp thu được không cần phải tách ra từng tín hiệu thành phần mà chúng được lấy mẫu rồi số hóa.

Trong thực tế, người ta không phải lấy mẫu liên tục mà chỉ lấy mẫu trong khoảng thời gian có xuất hiện điểm vang. Tốc độ lấy mẫu (sampling rate) cho biết mức độ dày thưa của các mẫu được lấy đối với mỗi điểm vang. Với số lượng mẫu nhất định cần lấy trong một điểm vang, tốc độ lấy mẫu tăng cho phép giảm thời gian lấy mẫu và ngược lại tốc độ lấy mẫu giảm làm kéo dài thời gian lấy mẫu.

k-không gian và phép biến đổi Fourier

Với mỗi tín hiệu số thu được, nghĩa là một điểm vang đã được số hóa, các mẫu của điểm vang này sẽ được ghi lại thành một hàng trong một cấu trúc dạng bảng có tên là k-không gian (k-space). Muốn có đủ dữ liệu tạo ra một bức ảnh của một lớp cắt, chúng ta phải lấy mẫu của nhiều điểm vang. Vì vậy trong k-không gian sẽ có nhiều hàng, mỗi hàng tương ứng với một điểm vang đã được đo. Hình 8 minh họa một điểm vang và kết quả lấy mẫu cùng với hàng tương ứng của điểm vang đó trong k-không gian.

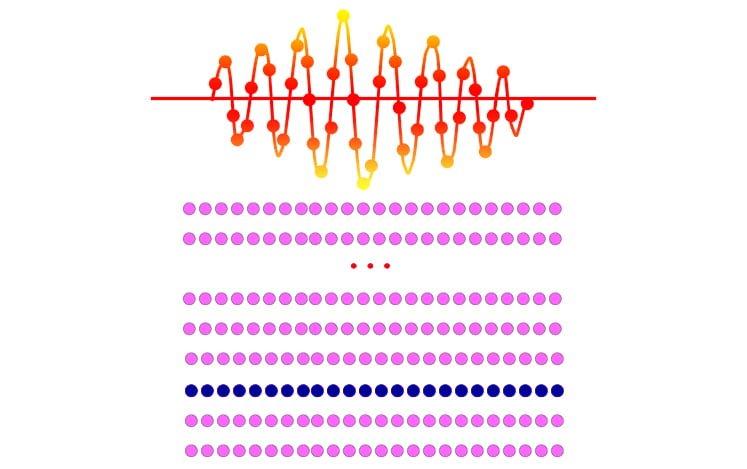
Hình 8: Lấy mẫu tín hiệu rồi điền vào một bảng hai chiều gọi là k-không gian. Trong k-không gian, mỗi mẫu là một con số, mỗi hàng tương ứng với một điểm vang được lấy mẫu. Hàng có các chấm đen biểu thị cho các mẫu được lấy từ tín hiệu (điểm vang) nằm ở phía trên của hình. Các hàng có các chấm xám là các mẫu đã lấy từ các điểm vang khác.

Bằng cách dùng một thuật toán gọi là phép biến đổi Fourier rời rạc hay thuật toán DFT (discrete Fourier transform), k-không gian sẽ được chuyển thành một ảnh cộng hưởng từ (Hình 9). Thuật toán này mặc dù khá phức tạp về mặt tính toán nhưng thực chất vẫn được bộ não của chúng ta thực hiện thường xuyên. Chẳng hạn khi nghe một bài hát, chúng ta chỉ nhận được một tín hiệu âm thanh tổng hợp. Sau khi truyền tín hiệu này lên não và được phân tích bằng “thuật toán Fourier”, chúng ta có thể phân biệt được đâu là tiếng hát của ca sỹ, đâu là tiếng đàn, đâu là tiếng trống. Và đối với một người có những kiến thức nhất định về âm nhạc, họ còn có thể biết được tín hiệu tổng hợp đó tạo ra hợp âm nào.

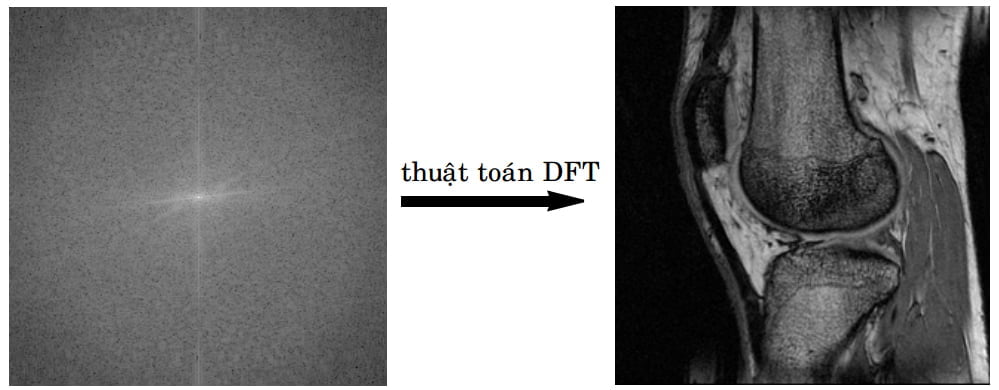
Hình 9: Thuật toán Fourier rời rạc (DFT), khi được cài đặt dưới dạng một chương trình máy tính, sẽ biến đổi k-không gian (bên trái) thành một hình cộng hưởng từ (bên phải). Chú ý rằng k-không gian được vẽ như trong Hình 9 này hoặc như trong Hình 8 chỉ để chúng ta dễ hình dung. Bản thân nó không có một “hình hài” nào cả.

Bây giờ, để có thể hiểu được cách thức hoạt động của nhiều chuỗi xung sẽ được bàn ở những phần sau, chúng ta cũng cần nắm chi tiết hơn một số tính chất của k-không gian. Trước tiên cần nhấn mạnh rằng k-không gian chỉ là một cấu trúc chứa dữ liệu thô mà chúng ta thu được khi chụp ảnh cộng hưởng từ. Mọi “điểm” dữ liệu trong k-không gian đều chứa đựng một phần thông tin của toàn bộ ảnh. Về mặt tổ chức, dữ liệu trong k-không gian cần được sắp đặt sao cho một chương trình máy tính (được viết để thực hiện thuật toán Fourier rời rạc) có thể dùng được nó để tái tạo lại chính xác hình ảnh của mặt cắt mà chúng ta đã chụp. Theo đấy, k-không gian của một hình cần có các tính chất sau:

1. Hàng trên cùng được điền bằng điểm vang có được khi áp dụng thang mã pha có cường độ mạnh nhất theo chiều dương (+Gp), hàng tiếp theo bên dưới được điền bằng điểm vang có được khi áp dụng thang mã pha yếu hơn, dần đến hàng giữa có thang từ bằng 0 rồi cường độ âm tăng dần cho đến hàng thấp nhất (-Gp). Hình 10 minh họa cho tính chất này (xem lại mục Thang từ mã hóa bằng pha Gp trong Phần 3).

Hình 10: Các điểm vang được điền vào k-không gian sao cho ở hàng trên cùng và dưới cùng là các điểm vang thu được khi áp dụng thang mã pha mạnh nhất (biểu thị bằng các chấm thật đen), còn ở hàng giữa là điểm vang có thang từ bằng 0 (biểu thị bằng các chấm mờ).

2. Mặc dù mỗi phần dữ liệu trong k-không gian đều chứa đựng thông tin của mọi điểm trong toàn bộ ảnh, thế nhưng vùng trung tâm chủ yếu chứa đựng thông tin cường độ và độ tương phản (mức độ trắng đen) còn vùng ngoại biên chủ yếu chứa đựng thông tin độ phân giải (mức độ rõ nét). Chẳng hạn với k-không gian của Hình 9, nếu chỉ dùng thông tin từ vùng trung tâm, chúng ta được một hình thấy rõ các vùng trắng đen nhưng không rõ nét (Hình 11), còn nếu chỉ dùng thông tin ở vùng ngoại biên, chúng ta được một hình thấy rõ các đường nét nhưng chẳng thấy rõ mức độ trắng đen (Hình 12).

3. k-không gian có hai trục đối xứng vuông góc với nhau tại tâm của nó. Nghĩa là hai nửa trên và dưới của k-không gian chứa các dữ liệu “tương tự nhau”; hai nửa trái và phải của nó cũng vậy. Tính đối xứng của hai nửa trên dưới có thể được dùng trong một kỹ thuật chụp có tên là kỹ thuật nửa Fourier (half-Fourier), trong đó chúng ta chỉ cần thu nhận hơn một nửa số hàng; phần còn lại chương trình máy tính sẽ tự “suy luận” và điền và Tương tự, tính chất đối xứng của hai nửa phải và trái cũng được sử dụng bằng cách chỉ cần lấy mẫu tín hiệu từ nửa thứ nhất của điểm vang; nửa sau sẽ được chương trình máy tính tự điền vào. Kỹ thuật lấy mẫu theo cách này được gọi là kỹ thuật nửa điểm vang (half-echo).

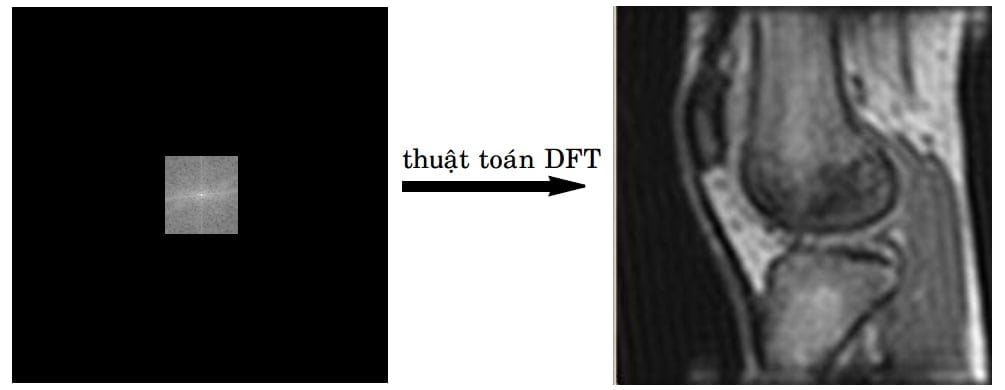
Hình 11: Dữ liệu ở vùng trung tâm của k-không gian trong Hình 9 mặc dù vẫn chứa đủ thông tin để cho ra hình ảnh nhìn chung vẫn giống như ảnh trong Hình 9 ở các vùng trắng đen nhưng không rõ nét vì không có thông tin được chứa trong vùng ngoại biên của k-không gian.

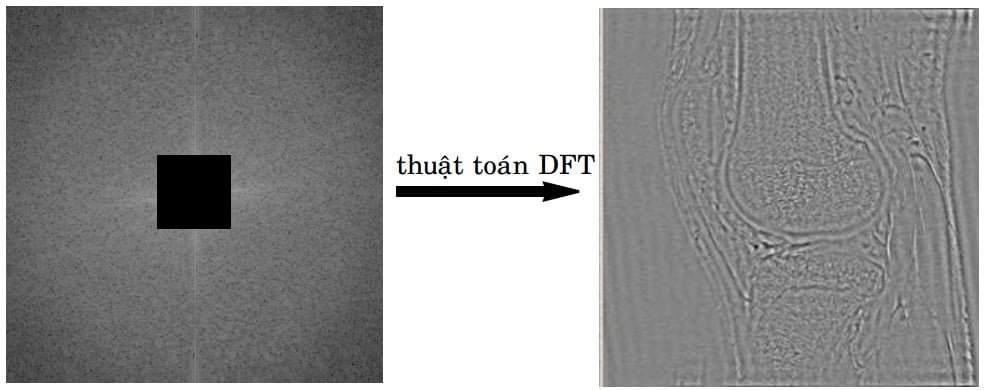
Hình 12: Dữ liệu ở vùng ngoại biên của k-không gian trong Hình 9 mặc dù vẫn chứa đủ thông tin để tạo ra hình ảnh có đường nét giống như của Hình 9 nhưng không có sự tương phản cần thiết giữa các cấu trúc vì thông tin về độ tương phản được lấy chủ yếu từ vùng trung tâm của k-không gian.

5. KỸ THUẬT CHỤP ẢNH BA CHIỀU

Kỹ thuật mã hóa vị trí không gian của Phần 3 cho phép phân định được các tín hiệu của các voxel trong lớp cắt cần khảo sát vốn đã được chuẩn bị trước bằng thang chọn lớp Gs. Với kỹ thuật này, tín hiệu thu được chính là tín hiệu phát ra từ một lớp cắt, và các thang mã tần Gf và bằng pha Gp cho phép xác định vị trí của các voxel trong mặt phẳng của lớp cắt theo hai chiều trong mặt phẳng đó. Kỹ thuật mã hóa và tạo ảnh như thế gọi là kỹ thuật chụp ảnh hai chiều hay kỹ thuật chụp 2D (2D hay 2-dimensional technique). Với kỹ thuật này, mỗi lần chúng ta chụp một lớp cắt riêng biệt nhờ vào thang chọn lớp Gs.

Trong kỹ thuật chụp ảnh ba chiều hay kỹ thuật chụp 3D, chúng ta không dùng thang chọn lớp Gs. Thay vì thế, toàn bộ khối cơ thể cần khảo sát được áp dụng một thang mã tần Gf. Thang từ này “cắt” khối cơ thể thành từng lát liên tục nhau, mỗi lát có tần số quay khác nhau, tăng dần theo chiều áp đặt thang từ. Sau đó với hai thang mã pha Gp, chúng ta có thể định vị được các voxel trong mỗi lát.

Khác với kỹ thuật chụp ảnh hai chiều, trong đó các lớp cắt thường có khoảng trống giữa chúng, kỹ thuật chụp ba chiều cho phép cắt được các lát khá mỏng và giữa hai lát kế cận không có khoảng trống. Vì vậy kỹ thuật chụp 3D rất có ích trong những trường hợp chúng ta cần cắt mỏng và liên tục để đánh giá các tổn thương nhỏ dễ bị bỏ sót khi chụp hai chiều, nhất là khi khoảng trống giữa hai lớp cắt lớn hơn kích thước của tổn thương. Ngoài ra, tỷ lệ tín hiệu/nhiễu SNR trong một hình được chụp ba chiều cao hơn so với hình được chụp hai chiều, cho ra ảnh chất lượng tốt hơn.

Cũng cần chú ý rằng kỹ thuật chụp ba chiều khác với kỹ thuật dựng hình ba chiều. Kỹ thuật chụp ba chiều là kỹ thuật cho phép đo tín hiệu của toàn khối thể tích vật cần chụp. Vì thế cũng giống như kỹ thuật chụp hai chiều, nó là một kỹ thuật chụp ảnh, tương tự như những kỹ thuật mà một người thợ thực hiện khi chụp ảnh. Ngược lại, dựng hình ba chiều là một kỹ thuật tái tạo lại hình ảnh ba chiều của vật cần chụp nhờ vào các tín hiệu đã thu được bằng một cách nào đó, có thể bằng kỹ thuật chụp hai chiều hoặc ba chiều. Vì vậy kỹ thuật dựng hình 3D có liên quan đến bước xử lý tín hiệu và dựng ảnh, tương tự như bước tráng và rửa phim của thợ chụp hình.

6. NHỮNG ĐIỂM CẦN GHI NHỚ

Trong phần này chúng ta đã xem xét nhiều khái niệm cơ sở của kỹ thuật chụp ảnh cộng hưởng từ. Những khái niệm này không chỉ được dùng trong kỹ thuật cộng hưởng từ mà còn được dùng phổ biến trong CT và những lĩnh vực hình ảnh học y học khác. Dưới đây là một số khái niệm quan trọng.

• Ảnh cộng hưởng từ là hình ảnh chụp một lớp cắt có một độ dày và một quang trường (diện tích bề mặt) nhất định. Nói cách khác, chúng ta không chụp bề mặt mà chụp một khối thể tích cơ thể.

• Mỗi lớp cắt được chia thành nhiều đơn vị thể tích gọi là voxel. Mỗi voxel có thể được xem là một khối thể tích mà các thiết bị chụp ảnh có thể phân định được tín hiệu từ đó phát Thể tích voxel càng nhỏ, khả năng phân định chi tiết càng tốt. Khả năng phân định này được gọi là độ phân giải không gian.

• Mỗi voxel sẽ được biểu diễn bằng một diện tích nhỏ trên ảnh gọi là pixel. Mỗi pixel cũng có thể được xem như diện tích nhỏ nhất có thể có ghi nhận được trên quang trường. Khi hiển thị trên màn hình hoặc in ra phim, mỗi pixel sẽ được trình bày bằng một điểm chấm (pixel thiết bị) có diện tích tùy thuộc vào khả năng hiển thị của thiết bị (độ phân giải thiết bị). Trong nhiều trường hợp, chúng ta có thể phóng đại ảnh bằng cách cho nhiều điểm chấm kế cận nhau cùng hiển thị một pixel.

• Để xác định được vị trí các voxel đã phát ra tín hiệu cộng hưởng từ, chúng ta cần dùng các thang từ. Thang chọn lớp được áp dụng trước khi phát xung, với mục đích là chuẩn bị tốc độ quay của các proton để xung kích thích chỉ tác dụng đối với lớp cắt cần khảo sát.

• Sau khi tắt xung kích thích, thang mã pha được áp dụng thật nhanh để làm thay đổi pha của các proton trong các voxel dọc theo trục của thang từ này (trục pha). Sự thay đổi pha một cách có hệ thống như thế cho phép định vị được các voxel dọc theo trục pha.

• Vào thời điểm gần đo tín hiệu (gần thời vang TE), thang mã tần được áp dụng, làm thay đổi tần số của các proton trong các voxel dọc theo thang từ này (trục tần số). Sự thay đổi tần số một cách có hệ thống này cho phép định vị được các voxel dọc theo trục tần số.

• Tín hiệu sau đó sẽ được lấy mẫu. Mỗi mẫu được biến đổi thành một con số. Đây được gọi là quá trình số hóa tín hiệu. Mỗi tín hiệu được lấy mẫu (điểm vang) sẽ được điền vào một hàng trong một bảng hai chiều gọi là k-không gian. Sau khi lấy mẫu nhiều lần và điền đầy vào k– không gian, chúng ta sử dụng một thuật toán gọi là thuật toán biến đổi Fourier rời rạc hay thuật toán DFT để biến đổi k-không gian thành ảnh cộng hưởng từ.

• Khi điền dữ liệu vào k-không gian, các hàng ở trên cùng và dưới cùng được điền bằng dữ liệu thu được khi thang mã pha có giá trị cao nhất (dương hoặc âm), trong khi đó các hàng ở vùng gần giữa được điền bằng dữ liệu thu được khi thang mã pha có cường độ gần như bằng zero.

• Trong k-không gian, tất cả mọi dữ liệu đều chứa đựng thông tin cho toàn bộ ảnh. Tuy nhiên dữ liệu ở vùng gần trung tâm của k-không gian được sử dụng chủ yếu để thiết lập độ tương phản của hình, trong khi đó dữ liệu ở vùng ngoại biên của k-không gian lại được sử dụng để tạo ra các đường nét và độ phân giải. Thông tin về độ phân giải (vùng trung tâm) là thông tin có được khi cường độ thang mã pha yếu nhất. Thông tin về độ phân giải (vùng ngoại biên) là thông tin tương ứng với cường độ thang mã pha mạnh nhất.

• Một tính chất quan trọng khác của k-không gian là tính đối xứng theo cả trục đứng và trục ngang. Tính đối xứng này trong nhiều trường hợp cho phép giảm bớt số hàng cần điền vào k-không gian (kỹ thuật nửa Fourier) hoặc giảm số mẫu cần lấy trong mỗi điểm vang (kỹ thuật nửa điểm vang).

• Khác với kỹ thuật chụp ảnh hai chiều chỉ cho phép cắt một khối cơ thể thành từng lớp cắt rời nhau, kỹ thuật chụp ảnh ba chiều cắt khối cơ thể thành các lớp mỏng liên tục nhau, giảm bớt khả năng bỏ sót các tổn thương nhỏ vốn có thể bị cắt hụt trong kỹ thuật chụp hai chiều.

Nguồn:

1. Trần Đức Quang (2008), Nguyên lý và kỹ thuật chụp cộng hưởng từ, Chương 4, NXB ĐHQG TPHCM, Trang 49-70.
2. Mriquestions.com
3. Radiopaedia.org
4. Materialise.com